In my last blog, I discussed how you can gain confidentiality and Language versatility on your deployed workload by keeping Enarx as runtime and setting WebAssembly as Compile target respectively.
Okay so with the help of Enarx keep you encrypted your data and blocked unauthorized access throughout the cycle and decrypted only when it was being processed with a unique key generated while constructing the enclave.
But what after this did Enarx disclose the data you kept confidential to the end verifier who asked for it? If No then how?
The answer is No. this was made possible with a technique named Zero-Knowledge proof it's like proving something is true without revealing the thing we're proving. let's try to understand ZKP.
Zero-Knowledge proof
Is a method for one party to cryptographically prove the another that they possess valid knowledge as a prover without actually revealing the underlying potentially sensitive data information to the verifier.
only that it exceeds a predefined threshold.
with enhanced privacy guarantees for users and institutions alike
There are two main kinds of zero-knowledge proofs – interactive and non-interactive.
Suppose Abacus(a calculating tool that has been used since ancient times) is not discovered yet and you are the founder and mastered this technique such that you can now calculate mentally. but want to prove to the world that with this method one can perform mathematical operations like Addition, subtraction, multiplication, and division, up to four digits within 30 seconds which is practically not possible with pen paper.
But the question is how will you prove this..? you cannot disclose the technique unless it gets patented on your name. since you don't trust anyone.
Non-Interactive Zero-Knowledge proof
as the name suggests you prove it in one go.
What you can do is ask people to give you similar mathematical problems to solve and set a timer returning them the answer after doing the mental calculation. and ask them to verify by calculating it with other methods. If it matches then they can verify your claim.
The scenario here is
Secret: Method of solving the mathematical operation within the time range.
Predefined threshold: Desired answer.
So you proved to the verifier that you know the method and your method remained unreviled. just the answer.
Interactive Zero-Knowledge proof
You prove this with regular interaction with the verifier.
The scenario here is
Secret: Method of solving the mathematical operation and the exact answer within the time range.
Predefined threshold: Desired answer range.
You can further modify the Threshold by not reviling the answer itself to the third person watching this verification process but instead giving the range in which your output falls. this can be done as the authority gave you multiple choices of number range to pick the correct one and they will verify that the range you chose is the correct one or not.
Then the question would be what if the prover did a guess among the choices.
If there are 4 options the chances of picking the one correctly for the first time would be 1:4.
If the prover picked the correct option a second time too then the probability will get twice that is 1:16,
with the third time, the probability becomes 1:64
4th time 1:256
5th time 1:1024
6th time 1:4096
.
.
.
And if you continued it 100 times the probability will drop to 1:1.6069380442589902755 x 10^60 and guess it's too much to verify someone.
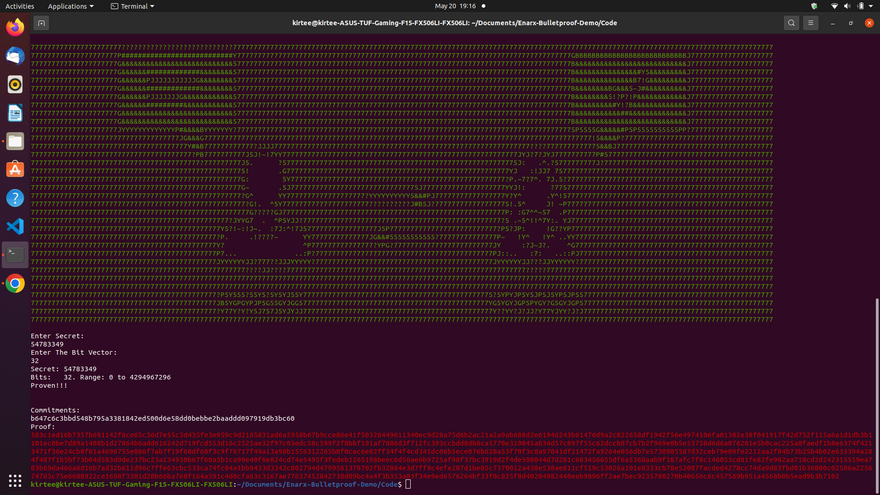
There is a similar demo with Enarx as a runtime performs to keep your data confidential by @shravi24 . git repo: Enarx-Bulletproof-Demo I'm demonstrating the same.
Enarx-Bulletproof-Demo
Environment Setup
now clone the repo Compile to WebAssembly and set Enarx as runtime.
git clone https://github.com/shravi24/Enarx-Bulletproof-Demo
cd Enarx-Bulletproof-Demo/Code
cargo build --target=wasm32-wasi
enarx run target/wasm32-wasi/debug/bp-test1.wasm
In this demo, you first enter a secret no and that number is kept in a range like 4 bit, 16 bit, 64 bit, and so on. and
then the verifier gives an input in bits which acts like a token or option respective to the example mentioned above if it matches program returns you the output as Proven!! and if not then Not Proven!!!
References:
How to prove you know a secret, without revealing what it is
Git repo of code
Enarx Docs







Top comments (0)